A Glitch in the Matrix (Redux)
In graduate school back in the 1980s, our class was dumbfounded by a blind classmate who nonchalantly performed an astounding act of mathematical gymnastics.
Over time, I’m reposting four or five early Bastiat’s Window essays (slightly edited), published before there were many readers (hence, “Redux”). Today’s story is about the majesty and mystery of the human mind, not about math—so don’t let the equations below scare you away. You won’t need to understand them any more than you have to understand the hieroglyphics in an article on Ancient Egypt.
The late Oliver Sacks wrote essays of poetic beauty on people with remarkable neurological gifts and deficits. A woman whose mind continually played melodies she had heard in infancy. An autistic artist of enormous and awe-inspiring talent (as shown in the video in the Lagniappe section below). The paradoxical sesquipedalianism of children with Williams Syndrome. People neurologically incapable of recognizing or enjoying music. A professional artist who is left utterly colorblind after an accident and reinvents his mastery of art. A Pacific atoll where colorblindness is endemic, thanks to a rogue gene. Among other questions, Sacks pondered the sources of genius. One of his most celebrated essays detailed the struggles and triumphs of autistic animal scientist Dr. Temple Grandin, who was a guest in 2021 on two of my podcasts—reposted here and here on Bastiat’s Window.
Sacks’s essays always have a peculiar and exhilarating effect on me. After finishing one, I feel that I know just a little bit less about the human mind than I knew before. After reading Sacks, I know some new facts and have a fine new story to share with friends. But with this new information, the mystery of the ghost in the machine is greater for me than it was just a few minutes earlier. It’s like watching a talented magician. The incomprehensibility is the thrill.
As a doctoral student in economics at Columbia University in the 1980s, I witnessed a small, but remarkable occurrence worthy of a Sacks essay. One of my fellow students performed an act of mental calculation that none of us could comprehend then—and which I still cannot comprehend 40+ years later.
Our professor, Martin Osborne, was a brilliant mathematical economist—and a good contender for the most congenial professor in the department. In his class on game theory, one of our fellow students was a charming Spaniard who was totally blind, or close to it. (I’ll call him Emilio, but I’m not certain that was his name.) Our classes—and Martin’s in particular—were heavily mathematical, with equation after equation. Professors would accommodate Emilio by sounding out the equations, rather than simply writing them on the board, as they usually did. Instead of simply writing something like this:
Martin would say out loud something like:
“z equals paren a-plus-b close paren … all divided by x-squared … multiply all of that by the sum from 0 to n of y-squared …”
Emilio would record the lecture on a cassette player and, if I remember correctly, his wife would transcribe it into Braille for him afterward. (Emilio’s wife was strikingly beautiful, and one of the department legends was that his best friend in the department had said, “Emilio, do you understand what a waste it is for you to be married to her?”)
One morning, Martin was doing matrix algebra. (Again, don’t worry if you don’t understand the concept. Just hang onto your hat and come along for the ride.) He wrote a 3-by-3 matrix that looked something like this (though I’m just making up the specific numbers):
Then Martin intended to write the inverse of that matrix, and he wrote something like this which, as you’ll learn was not quite the inverse:
(Again, don’t worry if you don’t know what an inverse matrix is. Just suffice it to say that it takes a painful number of steps to get from the original matrix to its inverse.) As usual, Martin sounded it out for Emilio:
The inverse of matrix A is a three-by-three matrix, and its rows are -24, 18, 5, then 20, 15, minus-4, and finally minus-5, 4, and 1.
Martin didn't show any of the steps involved in calculating the inverse matrix from the original. A moment after he finished, Emilio raised his hand and, in his gentle voice, said, “Eh … Martin?” Martin responded, “Yes, Emilio.” Emilio said, “In the second row, second column, I believe that should be minus-15 rather than a plus-15. Martin stared at him, looking dazed at the suggestion. He looked back at the board, and then finally turned around and said, “Well ... … … let’s see.”
This was before the era of laptops, so Martin went through the tedious process of calculating the number by hand. For those unschooled in matrix algebra, if you have a matrix like this:
you calculate the inverse matrix using the following array of equations—a time-consuming, mind-numbing task:
To check whether Emilio was correct, Martin would have calculated:
When he did, the answer was, indeed minus-15, and not plus-15. Staring at the board, Martin issued a mild expletive, then whirled around and asked, “How did you do that?” (Presumably, Emilio had done so for all nine numbers, since he correctly pointed out the only one that was wrong.)
Emilio just smiled in his signature Mona Lisa-level smile, and the rest of us understood the human mind just a little less than we had before that morning began. In those same years, Nadia Comăneci was dazzling the world with her Olympic gymnastics. I could watch her performance and describe what she had done, but I could never comprehend how the human body was capable of such control over Newtonian mechanics. I felt the same about Emilio’s instantaneous calculations.
In the famous 1993 essay, Temple Grandin told Oliver Sacks of her difficulty, as an autistic person, in comprehending human behavior: “Much of the time,” she said, “I feel like an anthropologist on Mars.” In contemplating Emilio’s internal calculations or Comăneci’s defiance of physics, I think I understand what Temple meant.
CAVEAT: This story was a recollection from four decades ago, so apologies if I misremembered any details. One possibility that I’ll mention is, while I thought it was a 3-by-3 matrix, it could have been a 2-by-2. That would make the calculations a good deal simpler—but still impossible for any of the other talented mathematicians in that room to do in their heads. The fact that Emilio had never SEEN that matrix, or seen ANY matrix, made his impromptu achievement all the more unfathomable for the rest of us.
When I first wrote this piece in 2022, our professor, Martin Osborne, and my classmate and great friend, Charlie Thomas, helped me refine this recollection. Thanks again to both of them.
THE INEXPLICABLE ARTISTRY OF STEPHEN WILTSHIRE
This video shows autistic artist Stephen Wiltshire’s capacity to see a vast, complex scene for an instant and then replicate it in enormous detail on a canvas.




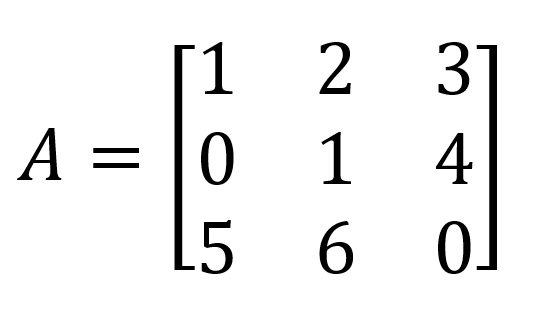

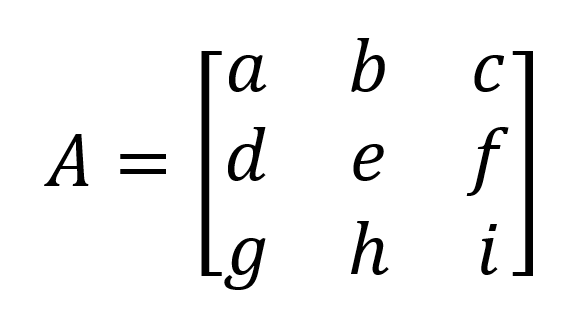

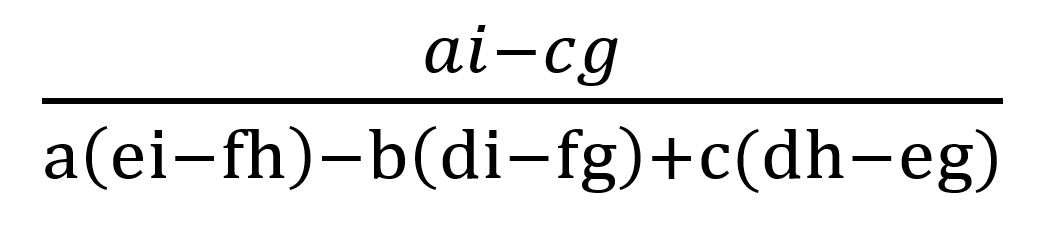

Since Martin gave both the matrix and its inverse, my guess is that, rather than calculating the inverse from scratch, Emilio simply multiplied the two matrices together to see if it produced the identity. Thus 1x(-24) + 2x20 +3x(-5) = 1 as it should, but 0x18 + 1x15 + 4x4 is not 1. But replace the 15 by -15 and it is 1. Still very impressive, as he has to do this for all 9 entries, and to notice that a simple change of sign will do it.
thank you for this article. it so reminds of me of what the psalmist says in Psalm 139, '.. "for I am fearfully and wonderfully made"