Polls Askew, Justice Denied, Lives in Peril, and the Subtle Truths of Double-Yolk Eggs
How three breakfasts suggested the fragility of statistics and the fallibility of statisticians.

My wife and I just got a fine lesson in statistical inference and the pitfalls of biased samples, courtesy of a carton of eggs from Nellie’s Free-Range. It delighted us, but also offered profound insight into why the legal system and enraged British public destroyed the life of a grieving mother, why a massive skyscraper came perilously close to demolishing a New York neighborhood, why an esteemed magazine failed spectacularly in the 1930s, and why scientific data should be simultaneously respected and suspected.
Shortly after publishing an essay on improbable events, I started making an omelet and beheld that rare and lovely oviparous four-leaf clover—the double-yolk egg. The next day, my wife cracked another egg and there was another double-yolk. Surely this was a rarity on the order of a case my essay had mentioned—two Bulgarian lotteries, a week apart, yielding the same six numbers (a 1-in-4 million happenstance). The next day, my wife cracked an egg and—yes—another double-yolk. Was this a Divine omen of End-Times?
I decided to research double-yolks and needed to go no farther than the Nellie’s egg carton and the Nellie’s website. The carton said the eggs were “jumbo” but mentioned nothing about double-yolks. But the website said:
WHAT CAUSES DOUBLE YOLKS?
Double yolk eggs are fairly rare (about 1/1000) and tend to be very, very large—in fact, they’re typically graded as “super jumbos” due to their size. These eggs primarily come from younger flocks that are just learning how to lay eggs.
All of the farm fresh eggs go through the sorting machine together and, once they are identified as super jumbos, are sent to the first packing station where they are hand packed because they are too big for the machine to pack. They are then packaged as jumbos, even though they are technically super jumbos. All day the hand packing station runs, filling jumbo cartons with super jumbos.
These Super Jumbos are over 50% double yolks. As these cartons are filled, they all go into the same case. So, even though they are rare, double yolk eggs often wind up in the same cartons.
So there we go. The probability of getting three double-yolk eggs in a row is one-in-a-billion [(1/1,000)×(1/1,000)×(1/1,000)=(1/1,000,000,000)]—but only if I’m drawing from the entire universe of chicken eggs. Given that over 50% of jumbos have double-yolks, the probability of three in a row is greater than one-in-eight [(1/2)×(1/2)×(1/2)=(1/8)]. As we’ll see, this offers extraordinarily important insights.
After I wrote the above, my wife cracked another egg, and it was a double-yoke again. From eggs in general, that would be a one-in-one-trillion occurrence. From Nellie’s Jumbos, it’s no less frequent than one-in-sixteen. Using another little trick called Bayesian Revision, I’m going to guess that it’s considerably more common with Nellie’s Jumbos than one-in-sixteen. This article argues that there is a one-in-a-trillion chance of your having a doppelgänger; just last week, I published an essay with photos of dozens of doppelgängers. Maybe the researcher’s definition is more rigid than mine; or maybe they don’t buy eggs from Nellie’s.
Let’s see what the eggs can teach us.
Figure 1: SELF-REFERENTIAL SAMPLING BIAS
Here’s a fine little graphic, adapted from one that appears on the Sampling Bias page on Wikipedia. It purports to show that a huge majority of people (99%) love responding to surveys. Of course, the humor is that most people who don’t like surveys didn’t answer this (fictitious) poll.
Figure 2: THE PERILS OF PAULINE
After Richard Nixon’s 1972 presidential election landslide, New Yorker film critic Pauline Kael unfairly gained a reputation as the ultimate bubble-dwelling left-winger, thanks to an apocryphal quote attributed to her:
“I can’t believe Nixon won. I don’t know anyone who voted for him.”
Kael was, indeed, a provincial, dwelling entirely within the closed sphere of New York City’s art world. But she was not an urban rube lacking self-awareness. What she actually said was creepy, but not clueless:
“I live in a rather special world. I only know one person who voted for Nixon. Where they are I don’t know. They’re outside my ken. But sometimes when I’m in a theater I can feel them.”
In our time, some pollsters consistently underestimate Republican voters, largely because Republicans (e.g., “shy Trump voters”) are more likely than Democrats to discard or refuse to take part in political surveys.
Figure 3: FASHION TRENDS
Sampling bias can also distort product marketing. In Figure 3, a hypothetical fashion catalogue goes awry by doing all of its research at a kombucha bar in Haight-Ashbury, San Francisco.
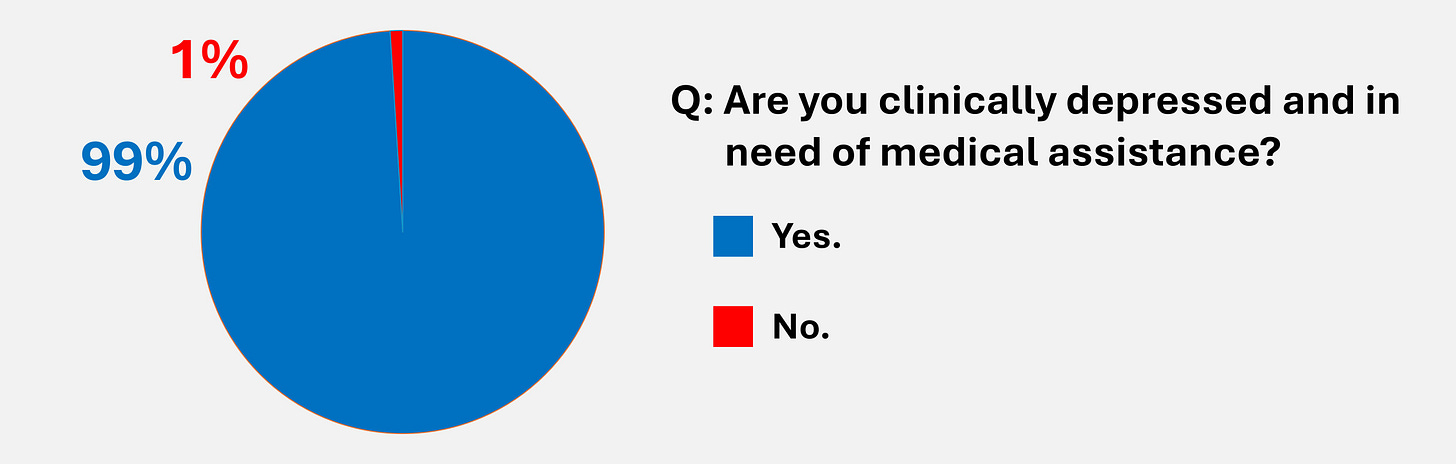
Figure 4: HIGH RATES OF DEPRESSION
Figure 4 represents a poorly executed study (fictitious) on the prevalence of clinical depression among college students. The result suggests an enormously high rate of depression, but the survey design is likely to have biased the results. People who are not depressed and are not in need of assistance may be prone to discard the the survey, whereas those in need of assistance may be likeliest to respond. (In the other direction, there may be also be some depressed people who do not respond.)
LITERARY DIGEST’S FACE-PLANT
In 1936, the prestigious, long-accurate Literary Digest poll predicted that Republican presidential candidate Alfred Landon would win the presidency with 57 percent of the popular vote and 370 electoral votes.” In fact, Franklin Roosevelt won 60.8% of the popular vote and 523 electoral votes, versus Landon’s 36.5% and 8 electoral votes. In hindsight, Literary Digest had drawn its sample from lists of Literary Digest readers, automobile owners, and those with telephones. Amidst the Great Depression, this strongly biased their sample toward wealthier Americans. Plus, people who disliked Roosevelt were far likelier to return their questionnaires than those who liked FDR. Public ridicule soon drove the magazine out of existence. Twelve years later, the Chicago Daily Tribune made similar polling errors, leading to an iconic photograph. Unlike Literary Digest, the Tribune lived on.

STATISTICIAN, PATHOLOGIST, JUDICIARY, AND CANCEL CULTURE DESTROY A GRIEVING MOTHER
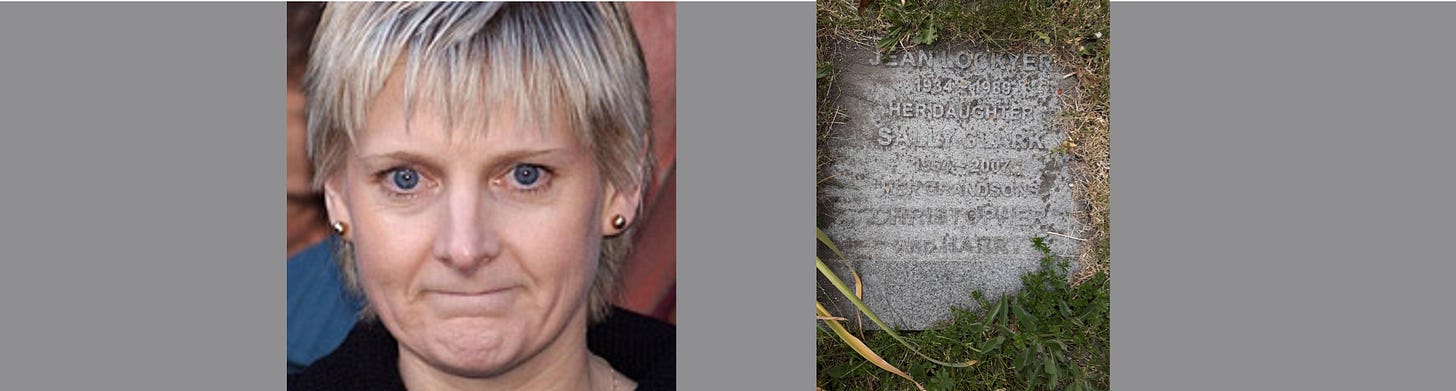
Failure to understand the double-yolk problem can lead to horrific miscarriages of justice. My 2022 post, “Experts with Statistics: Chimps with Machine Guns,” described an infamous miscarriage of justice in Britain. A twice-grieving mother was imprisoned and became a nationwide pariah because a statistician testifying against her failed to grasp the double-yolk problem. Here’s a shorter version of the facts.
In 1996 and 1998, solicitors Stephen and Sally Clark lost two children to sudden infant death syndrome (SIDS). Sally was accused of killing both children, ripped apart in the press, and jailed for several years. The only “evidence” against her was Professor Roy Meadow’s argument that the chance of a well-to-do couple losing two children to SIDS was extremely rare. He said 1-in-8,500 children die of SIDS, so the likelihood of two such deaths was (1/8,500)x(1/8,500) = (approximately 1/73,000,000). But, as with double-yolks in jumbo egg cartons, SIDS deaths are not independent events. Losing one child to SIDS actually implies a relatively high probability of losing a second child to SIDS (1-in-60, I read somewhere). Meadow’s logic was further undermined by the presence of a related statistical concept, the Prosecutor’s Fallacy—also discussed in my earlier article—along with a pathologist withholding exculpatory evidence, perhaps out of fear of siding with a publicly hated figure.
After four years, Sally Clark’s conviction was overturned and she left prison. The statistician and pathologist were sanctioned, though Meadow regained some court privileges. In 2004, a pediatrician working in child protective services was found guilty of professional misconduct after accusing Sally Clark’s husband, Stephen, of the murder of the two children. Sally Clark was emotionally destroyed by the saga and died in 2007 of alcohol poisoning.
STATISTICAL ERRORS NEARLY DESTROY A CITY
A statistician considering the likelihood of four double-yolks in a row will vastly underestimate the probability if he fails to realize that the eggs are jumbos. An analogous error in 1977 could have led to the collapse of a gigantic skyscraper and the destruction of a whole neighborhood of Manhattan. The story is told at Wikipedia, and there are loads of YouTube videos on the story, but here are the basics.
Citicorp Center, a 59-story tower, opened on the East Side of Manhattan in 1977. Its design was highly unconventional, with four supporting columns at the center of each wall—not at the corners. The architect and structural engineers assured that the building met standards established by the city building code—to guarantee that there was an extremely low probability of high winds toppling the building. But the code was designed for buildings with columns at the corners. Soon after the building went up, a graduate student writing a paper on the new tower suspected that there was an ominously high probability that winds could threaten the building. After reviewing her comments, the architect/engineer contemplated suicide but resisted and took responsibility. The city decided against evacuating the neighborhood or informing the public about the problem. Fortunately, the building’s unique design allowed engineers to add reinforcing structures inside the building rather than outside. So the city and engineers quietly bolstered the building, floor-by-floor, at night so outsiders wouldn’t notice. The job was quietly finished before hurricane season posed a threat.
As with double-yolk jumbos, FDR’s victory, or Sally Clark’s infant sons, the problem was fundamentally one of mistakenly assuming that a high-probability event was a low-probability event.
I figured I’d post a video about how double-yolks happen and found this one by “The Chicken Man” with “Texas Precision Poultry”—whatever that is. He explains that it’s something something something connected with the hen’s infundibulum (i.e., funnel-shaped egg cavity). This was a big revelation for me in that the only time I ever heard the word “infundibulum” was Kurt Vonnegut’s “chrono-synclastic infundibulum” in The Sirens of Titan. And I always assumed he just made the word up.




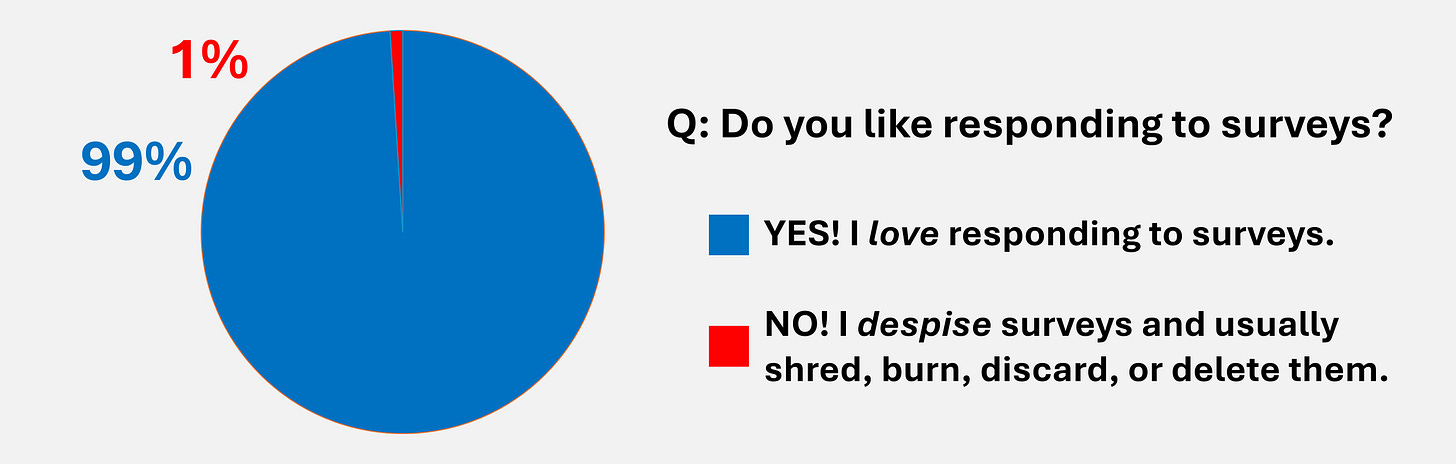



Valid statistics depends on random samples. Once you inject human perception into the sampling, abandon all hope ye who enter here.
I enjoyed your article. For my entire life, my wife has insisted on jumbo eggs. So, my perception is that double-yolks are quite common. And they are, because of the selection process that precedes my experience with the eggs.
You have to wonder how our perception of many things in our lives is biased by a selection process that we never see or are not even aware of.
As an engineer and a mathematician I am regularly appalled at the statistical ignorance of the media and the ordinary citizens in general. When I see some probability quoted in the public press I immediately doubt the rest of the article.